个人很喜欢的一个模型,原理很直观,准确率也不错。
随机森林(RF,Random Forest),一看就知道有随机和森林两个要素,森林里面当然要有树,这里的树就是决策树。简单理解就是用随机的方法搞很多决策树。
决策树
根据上文可以知道,要理解随机森林,首先得知道什么是决策树。
原理
决策树,Decision Tree,顾名思义,就是用来决策的树型结构。
树
树是一种常见的数据结构,大概就是有一个跟节点,从根节点出发经过子节点最后到达叶子节点。根节点只有一个,子节点和叶子节点可以有很多个,以下是一个树结构的例子:
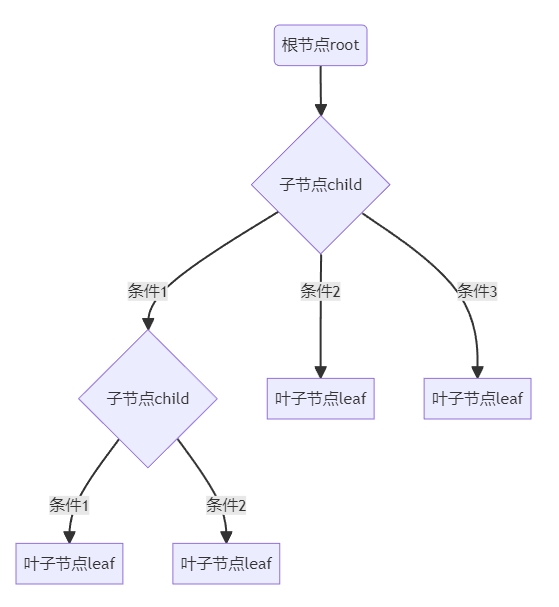
本来是用markdown搞的流程图,没想到网页没做相关的支持,很尴尬。截个图将就看看了,markdown代码如下:
```mermaid
graph TB
A(根节点root) --> B{子节点child}
B -->|条件1| C1{子节点child}
B -->|条件2| C2[叶子节点leaf]
B -->|条件3| C3[叶子节点leaf]
C1 -->|条件1| D1[叶子节点leaf]
C1 -->|条件2| D2[叶子节点leaf]
```决策树
把决策的行为放进树结构就可以了,看图就可以比较直观的理解了:
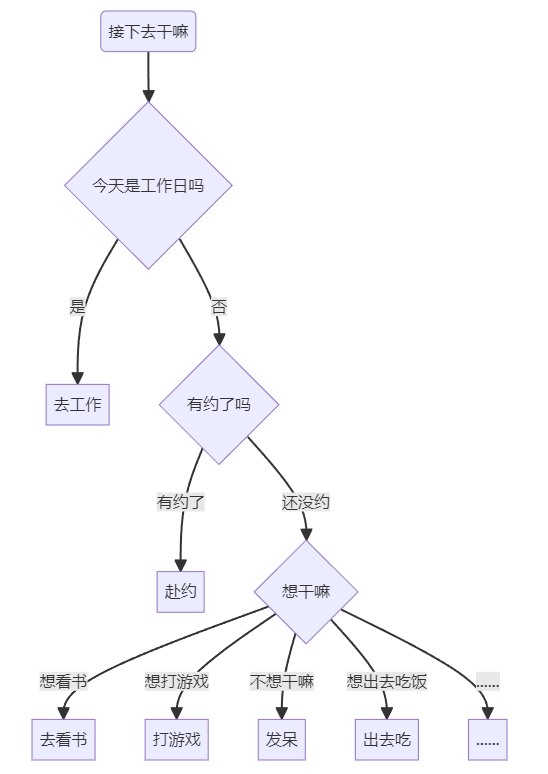
markdown代码:
```mermaid
graph TB
A(接下去干嘛) --> B{今天是工作日吗}
B -->|是| C1[去工作]
B -->|否| C2{有约了吗}
C2 -->|有约了| D1[赴约]
C2 -->|还没约| D2{想干嘛}
D2 -->|想看书| E1[去看书]
D2 -->|想打游戏| E2[打游戏]
D2 -->|不想干嘛| E3[发呆]
D2 -->|想出去吃饭| E4[出去吃]
D2 -->|……| E5[……]
```把特征(Feature,可以简单理解为自变量、属性这种东西)放到子节点上,把因变量放到叶子节点上,完事。
重要的特征(对结果影响大的)放在接近根节点位置,不重要的特征就往后放或者直接舍弃,关于特征的选择不同的决策树算法有不同的方法,这里就不展开了。
这里介绍用的是分类,实际上回归也是差不多的,关于回归和分类的关系和转化,以后看心情可能再写一篇吧。(咕,望天.jpg)
过拟合
Overfitting,也叫过度学习。是决策树最大的缺陷,虽然决策树也有减枝这样减少过拟合风险的方法,不过不如直接上随机森林~
过拟合有点类似于人在学习的时候不学习题目背后的规律而是死记硬背答案,造成的结果就是习题全对,考试完蛋。
用鼠标简单画了一下过拟合的情况:
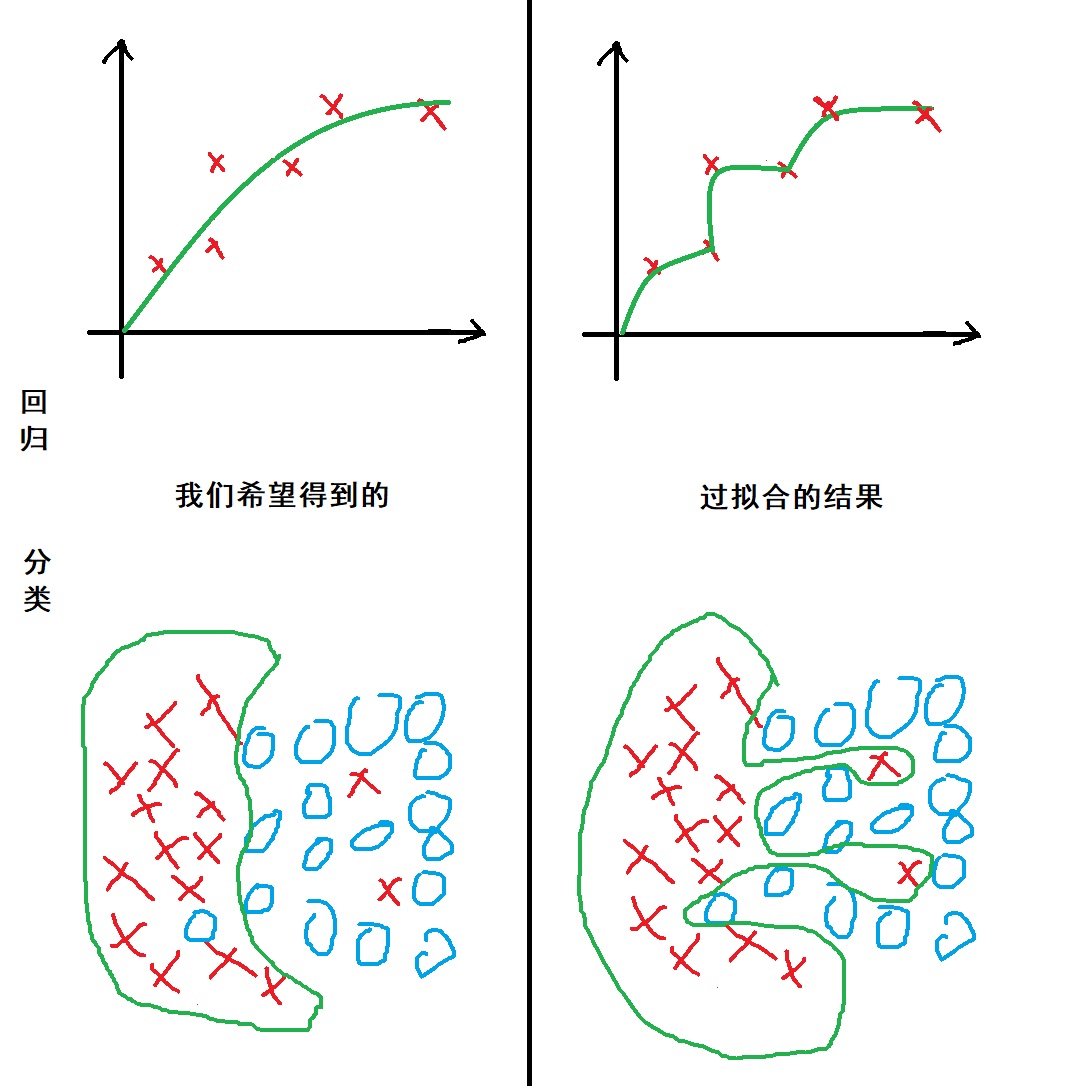
随机森林
知道决策树以后,随机森林就很好理解了。
一个人决策总会受限于知识水平、主观倾向等,那既然一个人做的决策不准,我找一个智囊团投票决定不就行了。随机森林就是类似这样的思路。
比如我们有一个包含了N条数据,每条数据有M个特征的数据集,训练随机森林时,随机从N条数据中取出n条,再从M个特征中选m个,用这n条数据和m个属性训练一棵决策树。这样的过程重复很多次,就形成了一个随机森林。
(关于RF的参数和调参太久没用忘了,有缘再说吧……)
实现
#加载模型
rf = RandomForestRegressor()
#训练数据集
X = train[data].values
y = train['y'].values
#测试数据集
test_X=test[data].values
test_y = test['y'].values
#模型训练
model = rf.fit(X,y)
#查看模型分数
model.score(X,y)
model.score(test_X,test_y)
#进行预测
pred = model.predict(pred_X)
